Difference between revisions of "Rainwater harvesting: Sizing and modeling"
Jump to navigation
Jump to search
Jenny Hill (talk | contribs) m (→Simple) |
Jenny Hill (talk | contribs) m |
||
| Line 14: | Line 14: | ||
Five percent of the average annual demand can be estimated: | Five percent of the average annual demand can be estimated: | ||
<math>D_{0.05} = P_{d} \times | <math>D_{0.05} = P_{d} \times n\times 18.25</math> | ||
{{plainlist|Where: | {{plainlist|Where: | ||
*''D<sub>0.05</sub>'' is five percent of the average annual demand (L) | *''D<sub>0.05</sub>'' is five percent of the average annual demand (L) | ||
*''P<sub>d</sub>'' is the daily demand per person (L) | *''P<sub>d</sub>'' is the daily demand per person (L) | ||
*'' | *''n'' is the number of occupants}} | ||
Then the following calculations are based upon two criteria: | Then the following calculations are based upon two criteria: | ||
| Line 25: | Line 25: | ||
When \(Y_{0.05}/D_{0.05}<0.33\), the storage volume required can be estimated: | When \(Y_{0.05}/D_{0.05}<0.33\), the storage volume required can be estimated: | ||
<math>V_{S} = | <math>V_{S} = A_{c} \times C_{vol,E}\times R_{d} \times e</math> | ||
{{plainlist|Where: | {{plainlist|Where: | ||
*''V<sub>S</sub>'' | *''V<sub>S</sub>'' is the volume of storage required (L) | ||
*''A'' | *''A<sub>c</sub>'' is the catchment area (m<sup>2</sup>) | ||
*''C<sub>vol,E</sub>'' | *''C<sub>vol,E</sub>'' is the design storm runoff coefficient for the catchment | ||
*''R<sub>d</sub>'' | *''R<sub>d</sub>'' is the design storm rainfall depth (mm), and | ||
*''e'' | *''e'' is the efficiency of the pre-storage filter.}} | ||
*Careful catchment selection means that the runoff coefficient, for | *Careful catchment selection means that the runoff coefficient, for an individual rainstorm event (''C<sub>vol, E</sub>'') should be 0.9 or greater. | ||
Finally, when \(0.33<Y_{0.05}/D_{0.05}<0.7\), the total storage required can be estimated by adding ''Y<sub>0.05</sub>'': | Finally, when \(0.33<Y_{0.05}/D_{0.05}<0.7\), the total storage required can be estimated by adding ''Y<sub>0.05</sub>'': | ||
Revision as of 18:58, 20 February 2018
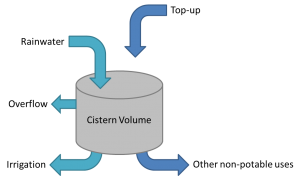
Simple[edit]
Five percent of the average annual yield can be estimated:
Where:
- Y0.05 is five percent of the average annual yield (L)
- Ac is the catchment area (m2)
- Cvol, A is the annual runoff coefficient for the catchment
- Ra is the average annual rainfall depth (mm)
- e is the efficiency of the pre-storage filter
- Filter efficiency (e) can be reasonably estimated as 0.9 pending manufacturer’s information.
- In a study of three sites in Ontario, STEP found the annual Cvol, A of the rooftops to be around 0.8 [1]. This figure includes losses to evaporation, snow being blown off the roof, and a number of overflow events.
Five percent of the average annual demand can be estimated:
Where:
- D0.05 is five percent of the average annual demand (L)
- Pd is the daily demand per person (L)
- n is the number of occupants
Then the following calculations are based upon two criteria:
- A design rainfall depth is to be captured entirely by the RWH system.
- The average annual demand (D) is greater than the average annual yield (Y) from the catchment.
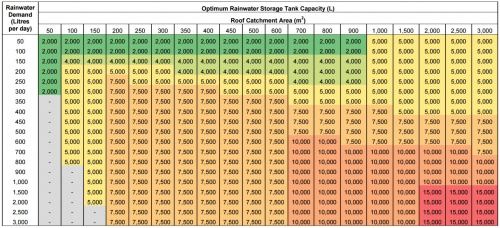
When \(Y_{0.05}/D_{0.05}<0.33\), the storage volume required can be estimated:
Where:
- VS is the volume of storage required (L)
- Ac is the catchment area (m2)
- Cvol,E is the design storm runoff coefficient for the catchment
- Rd is the design storm rainfall depth (mm), and
- e is the efficiency of the pre-storage filter.
- Careful catchment selection means that the runoff coefficient, for an individual rainstorm event (Cvol, E) should be 0.9 or greater.
Finally, when \(0.33<Y_{0.05}/D_{0.05}<0.7\), the total storage required can be estimated by adding Y0.05:
STEP Rainwater Harvesting Tool[edit]
The Sustainable Technologies Evaluation Program have produced a rainwater harvesting design and costing tool specific to Ontario. The tool is in a simple to use Excel format and is free to download.