Difference between revisions of "Grading"
Jump to navigation
Jump to search
Jenny Hill (talk | contribs) m |
Jenny Hill (talk | contribs) m |
||
| Line 1: | Line 1: | ||
{{float right|[[File:Theta.jpg|border|500 px]]}} | {{float right|[[File:Theta.jpg|border|500 px]]}} | ||
==Slope gradient== | ==Expressing slope== | ||
===Slope gradient=== | |||
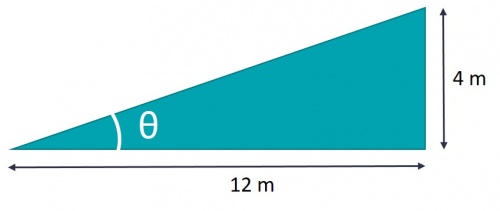
Slope gradients are expressed as Y:X where Y is a single unit of rise and X is the corresponding run. It can be calculated by dividing the rise by the run: | Slope gradients are expressed as Y:X where Y is a single unit of rise and X is the corresponding run. It can be calculated by dividing the rise by the run: | ||
e.g.:<math>\frac{rise}{run}=\frac{4\ m}{12\ m}=\frac{1}{3};we\ say\ the\ slope\ =1:3\ or\ 1\ in\ 3</math> | e.g.:<math>\frac{rise}{run}=\frac{4\ m}{12\ m}=\frac{1}{3};we\ say\ the\ slope\ =1:3\ or\ 1\ in\ 3</math> | ||
==Slope percentage== | ===Slope percentage=== | ||
Slope percentage is calculated similarly by dividing rise by run, but then multiplying by 100 to get a percentage: | Slope percentage is calculated similarly by dividing rise by run, but then multiplying by 100 to get a percentage: | ||
e.g.:<math>slope=\left (\frac{rise}{run}\right )\times 100=\left(\frac{4\ m}{12\ m}\right)\times 100= 33\%</math> | e.g.:<math>slope=\left (\frac{rise}{run}\right )\times 100=\left(\frac{4\ m}{12\ m}\right)\times 100= 33\%</math> | ||
==Slope in degrees== | ===Slope in degrees=== | ||
Expressing a slope in degrees requires using the ''inverse tangent'' trigonometric function. | Expressing a slope in degrees requires using the ''inverse tangent'' trigonometric function. | ||
e.g.:<math>\tan \theta =\left ( \frac{4\ m}{12\ m} \right ); \theta =\tan^{-1}\left ( 0.33 \right )=18.3^{\circ}</math> | e.g.:<math>\tan \theta =\left ( \frac{4\ m}{12\ m} \right ); \theta =\tan^{-1}\left ( 0.33 \right )=18.3^{\circ}</math> | ||
<ref>Ontario. O. Reg. 191/11: INTEGRATED ACCESSIBILITY STANDARDS, 2011. https://www.ontario.ca/laws/regulation/r11191.</ref> | ==Accessibility== | ||
The Accessibility for Ontarians with Disabilities Act<ref>Ontario. O. Reg. 191/11: INTEGRATED ACCESSIBILITY STANDARDS, 2011. https://www.ontario.ca/laws/regulation/r11191.</ref> provides a foundation, a bare minimum to which public spaces must be designed. | |||
{|class= "wikitable" "style=text-align: center;" | {|class= "wikitable" "style=text-align: center;" | ||
Revision as of 17:51, 19 October 2018
Expressing slope
Slope gradient
Slope gradients are expressed as Y:X where Y is a single unit of rise and X is the corresponding run. It can be calculated by dividing the rise by the run: e.g.:
Slope percentage
Slope percentage is calculated similarly by dividing rise by run, but then multiplying by 100 to get a percentage: e.g.:
Slope in degrees
Expressing a slope in degrees requires using the inverse tangent trigonometric function. e.g.:
Accessibility
The Accessibility for Ontarians with Disabilities Act[1] provides a foundation, a bare minimum to which public spaces must be designed.
| Use | Extreme range (%) | Desirable range (%) |
|---|---|---|
| Public Streets | 0.5 - 10 | 1 - 8 |
| Private streets | 0.5 - 20 | 1 - 12 |
| Service lanes | 0.5 - 15 | 1 - 10 |
| Parking areas | 0.5 - 8 | 1 - 5 |
| Parking ramps | up to 20 | up to 15 |
| Collector walks | 0.5 - 12 | 1 - 8 |
| Entrance walks | 0.5 - 8 | 1 - 4 |
| Pedestrian ramps | up to 12 | up to 8 |
| Stairs | 25 - 50 | 33 - 50 |
| Game courts | 0.5 - 2 | 0.5 - 1.5 |
| Paved gutters | 0.25 - 100 | 1 - 50 |
| Grassed swales | 0.5 - 15 | 2 - 10 |
| Terraces and sitting areas | 0.5 - 3 | 1 - 2 |
| Grassed banks | up to 50 | up to 33 |
| Planted banks | up to 100 | up to 50 |
- ↑ Ontario. O. Reg. 191/11: INTEGRATED ACCESSIBILITY STANDARDS, 2011. https://www.ontario.ca/laws/regulation/r11191.
- ↑ Strom, S., Nathan, K., Woland, J. Site Engineering for Landscape Architects (6th Ed.) 2013, Wiley and Sons